已知椭圆
的右焦点为F2（1，0），点
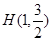在椭圆上.
（1）求椭圆方程；
（2）点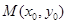
在圆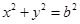
上，M在第一象限，过M作圆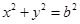的切线交椭圆于P、Q两点，问|F2P|+|F2Q|+|PQ|是否为定值？如果是，求出定值，如不是，说明理由.
的值。
的周长为
，求扇形的半径，圆心角各取何值时，此扇形的面积最大？
的终边上的点
与
关于
轴对称
，角
的终边上的点
与
关于直线
对称，求
之值．
，（1）求
的值。
的值。
求
的值。推荐套卷
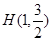已知椭圆的右焦点为F2（1，0），点 在椭圆上.
（1）求椭圆方程；
（2）点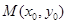在圆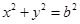上，M在第一象限，过M作圆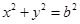的切线交椭圆于P、Q两点，问|F2P|+|F2Q|+|PQ|是否为定值？如果是，求出定值，如不是，说明理由.
粤公网安备 44130202000953号