已知四棱锥P-ABCD的底面ABCD是等腰梯形，AB∥CD，且AC⊥BD，AC与BD交于O，PO⊥底面ABCD，PO＝2，AB＝2CD＝2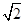
，E，F分别是AB，AP的中点．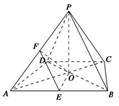
(1)求证：AC⊥EF；
(2)求二面角F-OE-A的余弦值．
相关试题
平方米的矩形堆料场，一边可以利用原有的墙壁，其他三边需要砌新的墙壁，问堆料场的长和宽各为多少时，才能使砌墙所用的材料最省？
在
处取得极值，且在
点处的切线与直线
平行．
的解析式； (2）求函数
的单调递增区间及极值；
的最值.
满足
， 
；
，直线
，
，
围成图形的面积S.
，实数
取什么值时，
是实数；（2复数推荐套卷
已知四棱锥P-ABCD的底面ABCD是等腰梯形，AB∥CD，且AC⊥BD，AC与BD交于O，PO⊥底面ABCD，PO＝2，AB＝2CD＝2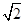，E，F分别是AB，AP的中点．
(1)求证：AC⊥EF；
(2)求二面角F-OE-A的余弦值．
粤公网安备 44130202000953号