某学生参加某高校的自主招生考试，须依次参加A，B，C，D，E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试．已知每一项测试都是相互独立的，该生参加A，B，C，D四项考试不合格的概率均为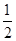
，参加第五项不合格的概率为
.
(1)求该生被录取的概率；
(2)记该生参加考试的项数为X，求X的分布列和期望．
相关试题
.（Ⅰ）若曲线
在点
处与直线
相切，求
的值；（Ⅱ）求函数
的单调区间与极值点.
的值域
的导数
其中
时，求曲线
处的切线的斜率；
时，求函数
的单调区间与极值。
; (2) 一年期优惠利率为多少时,利息差最大?推荐套卷
某学生参加某高校的自主招生考试，须依次参加A，B，C，D，E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试．已知每一项测试都是相互独立的，该生参加A，B，C，D四项考试不合格的概率均为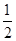，参加第五项不合格的概率为.
(1)求该生被录取的概率；
(2)记该生参加考试的项数为X，求X的分布列和期望．
粤公网安备 44130202000953号