（本小题满分9分）要制做一个体积为72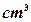
的长方体带盖箱子，并且使长宽之比为
，设箱子的表面积为
，宽为
。
（1）写出箱子的表面积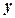
关于宽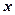
的函数解析式，并写出函数的定义域；
（2）求箱子的表面积的最小值及取得最小值时的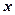的值。
相关试题
满足
，
是
，
的等差中项。
，求数列
的前
项和
。
中，若
。
的大小；
，
，求
，
的值。
是等差数列，其中
，
。
…
的值。
中，
分别为内角
所对的边长，
，
，
，求：
的大小；
上的高。
都在区间
上有定义，对任意
，都有
成立，则称函数
为区间
上的“伙伴函数”，求
的范围。
是否为区间
上的“伙伴函数”？
为区间
上的“伙伴函数”，求
的取值范围相关知识点
推荐套卷
（本小题满分9分）要制做一个体积为72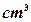的长方体带盖箱子，并且使长宽之比为，设箱子的表面积为，宽为。
（1）写出箱子的表面积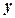关于宽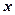的函数解析式，并写出函数的定义域；
（2）求箱子的表面积的最小值及取得最小值时的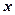的值。
粤公网安备 44130202000953号