已知函数
的图象的一个最高点为
与之相邻的与
轴的一个交点为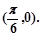
（1）求函数
的解析式；
（2）求函数的单调减区间和函数图象的对称轴方程；
（3）用“五点法”作出函数在长度为一个周期区间上的图象.
相关试题
△ABC中,角A,B,C的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos2B=1.
(1)求证:a,b,c成等差数列;(2)若C=
,求
的值.
中，
成等比数列, 公比为
, 求证：
．
为第二象限角，且
，求
的值.
·an(n∈N+).
,求证:c1+c2+c3+…+cn<
.相关知识点
推荐套卷
已知函数的图象的一个最高点为与之相邻的与轴的一个交点为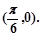
（1）求函数的解析式；
（2）求函数的单调减区间和函数图象的对称轴方程；
（3）用“五点法”作出函数在长度为一个周期区间上的图象.
△ABC中,角A,B,C的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos2B=1.
(1)求证:a,b,c成等差数列;(2)若C=,求的值.
粤公网安备 44130202000953号