某公司欲建连成片的网球场数座,用288万元购买土地20000平方米,每座球场的建筑面积为1000平方米,球场每平方米的平均建筑费用与所建的球场数有关,当该球场建n座时,每平方米的平均建筑费用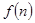 表示,且
表示,且 (其中
(其中 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.
(1)为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几座网球场?
(2)若球场每平方米的综合费用不超过820元,最多建几座网球场?
相关知识点
推荐套卷
某公司欲建连成片的网球场数座,用288万元购买土地20000平方米,每座球场的建筑面积为1000平方米,球场每平方米的平均建筑费用与所建的球场数有关,当该球场建n座时,每平方米的平均建筑费用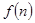 表示,且
表示,且 (其中
(其中 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.
(1)为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几座网球场?
(2)若球场每平方米的综合费用不超过820元,最多建几座网球场?