(1)已知点 和
和 ,过点
,过点 的直线
的直线 与过点
与过点 的直线
的直线 相交于点
相交于点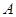 ,设直线
,设直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,如果
,如果 ,求点
,求点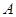 的轨迹;
的轨迹;
(2)用正弦定理证明三角形外角平分线定理:如果在 中,
中, 的外角平分线
的外角平分线 与边
与边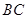 的延长线相交于点
的延长线相交于点 ,则
,则 .
.
推荐套卷
(1)已知点 和
和 ,过点
,过点 的直线
的直线 与过点
与过点 的直线
的直线 相交于点
相交于点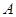 ,设直线
,设直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,如果
,如果 ,求点
,求点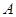 的轨迹;
的轨迹;
(2)用正弦定理证明三角形外角平分线定理:如果在 中,
中, 的外角平分线
的外角平分线 与边
与边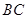 的延长线相交于点
的延长线相交于点 ,则
,则 .
.