如图,已知椭圆 :
: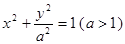 的离心率为
的离心率为  ,点
,点 为其下焦点,点
为其下焦点,点 为坐标原点,过
为坐标原点,过 的直线
的直线  :
: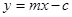 (其中
(其中 )与椭圆
)与椭圆 相交于
相交于 两点,且满足:
两点,且满足: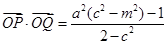 .
.
(1)试用  表示
表示 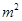 ;
;
(2)求  的最大值;
的最大值;
(3)若 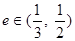 ,求
,求  的取值范围.
的取值范围.
推荐套卷
如图,已知椭圆 :
: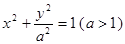 的离心率为
的离心率为  ,点
,点 为其下焦点,点
为其下焦点,点 为坐标原点,过
为坐标原点,过 的直线
的直线  :
: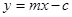 (其中
(其中 )与椭圆
)与椭圆 相交于
相交于 两点,且满足:
两点,且满足: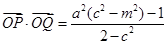 .
.
(1)试用  表示
表示 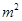 ;
;
(2)求  的最大值;
的最大值;
(3)若 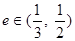 ,求
,求  的取值范围.
的取值范围.