学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(Ⅰ)求水面宽;
(Ⅱ)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?
(Ⅲ)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
相关知识点
推荐套卷
 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学. 社区的概率;
社区的概率; 为四名同学中到
为四名同学中到 的值.
的值. 的最小正周期为
的最小正周期为 .
. 时,求函数
时,求函数 的最小值;
的最小值; ,若
,若 ,且
,且 ,求
,求 的值.
的值. 个实数组成的
个实数组成的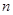 行
行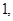
 ,
,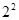 ,
,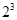

 ,再将首项为
,再将首项为 公比为
公比为 的数列
的数列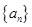 依次填入第一列的空格内,然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规律填写其它空格
依次填入第一列的空格内,然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规律填写其它空格
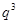

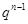
 .试用
.试用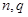 表示
表示 的值;
的值;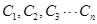 ,记为数列
,记为数列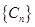 .
.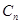 ;
;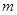 项
项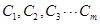 (
(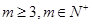 )成等比数列?若能找到,
)成等比数列?若能找到,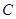 的离心率
的离心率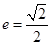 ,长轴的左右端点分别为
,长轴的左右端点分别为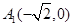 ,
, .
.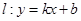 与曲线
与曲线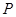 ,且与直线
,且与直线 相交于点
相交于点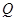 .
.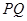 为直径的圆过定点
为直径的圆过定点 .
.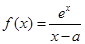 ,(其中常数
,(其中常数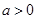 )
)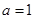 时,求曲线在
时,求曲线在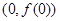 处的切线方程;
处的切线方程; 使得不等式
使得不等式 成立,求
成立,求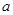 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号