在平面直角坐标系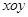 中,已知
中,已知 分别是椭圆
分别是椭圆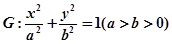 的左、右焦点,椭圆
的左、右焦点,椭圆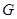 与抛物线
与抛物线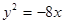 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
.
(Ⅰ)求椭圆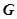 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆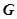 相交于
相交于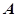 、
、 两点,若
两点,若 (
(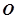 为坐标原点),试判断直线
为坐标原点),试判断直线 与圆
与圆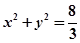 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
相关知识点
推荐套卷
在平面直角坐标系 中,已知
中,已知 分别是椭圆
分别是椭圆 的左、右焦点,椭圆
的左、右焦点,椭圆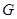 与抛物线
与抛物线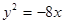 有一个公共的焦点,且过点
有一个公共的焦点,且过点 .
.
(Ⅰ)求椭圆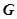 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆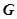 相交于
相交于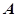 、
、 两点,若
两点,若 (
(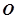 为坐标原点),试判断直线
为坐标原点),试判断直线 与圆
与圆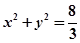 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.