已知函数
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数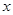 ,
,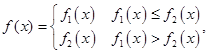
(1)求证:当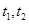 满足条件
满足条件 时,对于
时,对于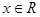 ,
,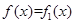 ;
;
(2)设 是两个实数,满足
是两个实数,满足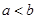 ,且
,且 ,若
,若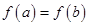 ,求函数
,求函数 在区间
在区间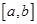 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间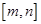 的长度定义为
的长度定义为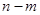 )
)
相关知识点
推荐套卷
已知函数
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数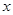 ,
,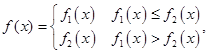
(1)求证:当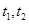 满足条件
满足条件 时,对于
时,对于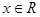 ,
,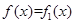 ;
;
(2)设 是两个实数,满足
是两个实数,满足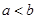 ,且
,且 ,若
,若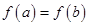 ,求函数
,求函数 在区间
在区间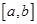 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间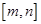 的长度定义为
的长度定义为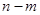 )
)