把两个直角三角形如图(1)放置,使∠ACB与∠DCE重合,AB与DE相交于点O,其中∠DCE=90°,∠BAC=45°,AB=6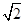
cm,CE="5cm," CD=10cm．
（1）图1中线段AO的长= cm；DO= cm
图1
（2）如图2,把△DCE绕着点C逆时针旋转α度（0°＜α＜90°）得△D1CE1,D1C与AB相交于点F,若△BCE1恰好是以BC为底边的等腰三角形,求线段AF的长．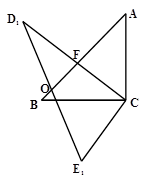
图2
相关试题
如图，
两地之间有一座山，汽车原来从
地到
地须经
地沿折线
行驶，现开通隧道后，汽车直接沿直线
行驶．已知
，
，
，则隧道开通后，汽车从地到地比原来少走多少千米？（结果精确到
）（参考数据：
，
）
四人随机分成甲、乙两组参加羽毛球比赛，每组两人．
在甲组的概率是多少？
都在甲组的概率是多少？
中，
，
，
，
相交于点
，
；
，
；
，
，求菱形某养鸡场分3次用鸡蛋孵化出小鸡，每次孵化所用的鸡蛋数、每次的孵化率（孵化率
）分别如图1，图2所示：
（1）求该养鸡场这3次孵化出的小鸡总数和平均孵化率；
（2）如果要孵化出2000只小鸡，根据上面的计算结果，估计该养鸡场要用多少个鸡蛋？
．相关知识点
推荐套卷
粤公网安备 44130202000953号