某品牌汽车4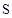
店经销
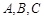三种排量的汽车，其中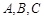三种排量的汽车依次有５，4，3款不同车型．某单位计划购买3辆不同车型的汽车，且购买每款车型等可能．
(1)求该单位购买的3辆汽车均为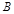
种排量汽车的概率；
(2)记该单位购买的3辆汽车的排量种数为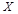
，求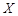
的分布列及数学期望．
相关试题
内有一点
，
为过点
且倾斜角为
的弦，
;
，求点
、
距离的比为
的点的轨迹，则求此曲线的方程.
且到原点的距离等于1的直线方程.
，且与两坐标轴构成周长为10的三角形的直线方程推荐套卷
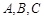某品牌汽车4店经销三种排量的汽车，其中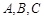三种排量的汽车依次有５，4，3款不同车型．某单位计划购买3辆不同车型的汽车，且购买每款车型等可能．
(1)求该单位购买的3辆汽车均为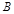种排量汽车的概率；
(2)记该单位购买的3辆汽车的排量种数为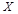，求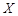的分布列及数学期望．
粤公网安备 44130202000953号