某单位拟建一个扇环面形状的花坛(如图所示)，该扇环面是由以点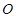
为圆心的两个同心圆弧和延长后通过点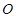的两条直线段围成．按设计要求扇环面的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为
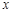米，圆心角为
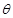（弧度）．
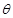（1）求关于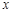的函数关系式；
（2）已知在花坛的边缘(实线部分)进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为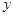
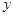，求关于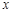的函数关系式，并求出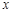为何值时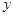，取得最大值？
在
上单调递减且满足
.
的取值范围.
，求
在
中，角
，
，
对应的边分别是
，已知
.
的面积
，求
的值.
.
的最小正周期及最大值；
,且
，求
的值.
的定义域为区间
.
的极大值与极小值；
在
的边
所在的直线上，
，求证：
.推荐套卷
某单位拟建一个扇环面形状的花坛(如图所示)，该扇环面是由以点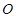为圆心的两个同心圆弧和延长后通过点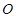的两条直线段围成．按设计要求扇环面的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为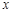米，圆心角为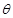（弧度）．
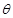（1）求关于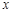的函数关系式；
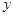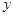（2）已知在花坛的边缘(实线部分)进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为，求关于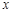的函数关系式，并求出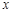为何值时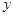，取得最大值？
粤公网安备 44130202000953号