如图,点C在以AB为直径的半圆O上,以点A为旋转中心,以∠β(0°<β<90°)为旋转角度将B旋转到点D,过点D作DE⊥AB于点E,交AC于点F,过点C作圆O的切线交DE于点G。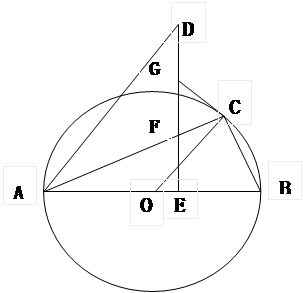
(1)求证:∠GCA=∠OCB;
(2)设∠ABC=m°,求∠DFC的值;
(3)当G为DF的中点时,请探究∠β与∠ABC的关系,并说明理由。
相关知识点
推荐套卷
如图,点C在以AB为直径的半圆O上,以点A为旋转中心,以∠β(0°<β<90°)为旋转角度将B旋转到点D,过点D作DE⊥AB于点E,交AC于点F,过点C作圆O的切线交DE于点G。
(1)求证:∠GCA=∠OCB;
(2)设∠ABC=m°,求∠DFC的值;
(3)当G为DF的中点时,请探究∠β与∠ABC的关系,并说明理由。