已知：直角梯形ABCD中，DC⊥BC，AD∥BC，AD=AB=5，BC=8.动点P以1个单位/秒的速度从C开始，沿C—D—A方向运动，到达点A时停止.
（1）设△BCP的面积为y，运动的时间为t秒. 求y关于t的函数关系式，并写出t的范围；
（2）连接AP，当点P在CD上时，求在第几秒时，△ABP的面积与△BCP的面积相等？
（3）若在点P从点C出发的同时，另一动点M从A开始沿着A—D—C方向运动，运动速度为2个单位/秒. 求当P、M相遇时，△BCP的面积？
相关试题
某商场销售一批名牌服装，平均每天可售出20件，每件盈利40元，为了增加盈利，商场决定采取适当的降价措施，经调查发现．如果每件服装每降低1元，商场平均每天可多售出2件．若商场平均每天要盈利1200元，问每件服装应降价多少元？
．求：如图，△ABC中，∠B=10°，∠ACB=20°，AB=4cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD的中点．
（1）指出旋转中心，并求出旋转的度数；
（2）求出∠BAE的度数和AE的长．
相关知识点
推荐套卷
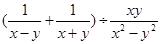
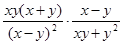
粤公网安备 44130202000953号