已知点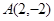 和点
和点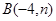 在抛物线
在抛物线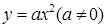 上.
上. 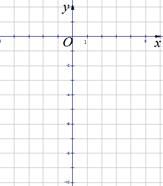
(1)求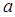 的值及点
的值及点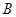 的坐标;
的坐标;
(2)点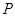 在
在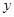 轴上,且满足△
轴上,且满足△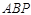 是以
是以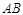 为直角边的直角三角形,求点
为直角边的直角三角形,求点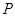 的坐标;
的坐标;
(3)平移抛物线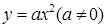 ,记平移后点A的对应点为
,记平移后点A的对应点为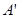 ,点B的对应点为
,点B的对应点为 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,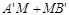 最短,求此时抛物线的函数解析式.
最短,求此时抛物线的函数解析式.
相关知识点
推荐套卷
已知点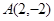 和点
和点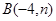 在抛物线
在抛物线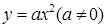 上.
上. 
(1)求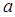 的值及点
的值及点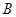 的坐标;
的坐标;
(2)点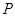 在
在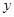 轴上,且满足△
轴上,且满足△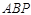 是以
是以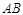 为直角边的直角三角形,求点
为直角边的直角三角形,求点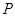 的坐标;
的坐标;
(3)平移抛物线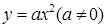 ,记平移后点A的对应点为
,记平移后点A的对应点为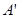 ,点B的对应点为
,点B的对应点为 . 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,
. 点M(2,0)在x轴上,当抛物线向右平移到某个位置时,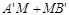 最短,求此时抛物线的函数解析式.
最短,求此时抛物线的函数解析式.