如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：
①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（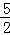
，y2）是抛物线上两点，则y1＞y2．其中说法正确的是（ ）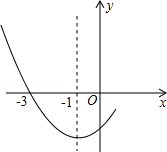
| A．①② | B．②③ | C．①②④ | D．②③④ |
相关试题
相关知识点
推荐套卷
如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：
①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1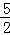），（，y2）是抛物线上两点，则y1＞y2．其中说法正确的是（ ）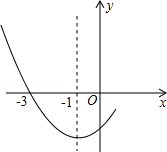
| A．①② | B．②③ | C．①②④ | D．②③④ |
粤公网安备 44130202000953号