已知函数f(x)＝ax2＋bx＋1(a，b为实数)，x∈R，F(x)＝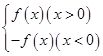
(1)若f(－1)＝0，且函数f(x) ≥0的对任意x属于一切实数成立，求F(x)的表达式；
(2)在 (1)的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围；
相关试题
。
，使得
处取极值？试证明你的结论；
上是减函数，求实数
的首项为
（1）若
，求证：数列
是等比数列；（2）若
，求数列
的前
项和.
中，
底面
，
，
，点
、
分别是
、
的中点.
；（2）求二面角
的余弦值。
推荐套卷
已知函数f(x)＝ax2＋bx＋1(a，b为实数)，x∈R，F(x)＝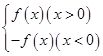
(1)若f(－1)＝0，且函数f(x) ≥0的对任意x属于一切实数成立，求F(x)的表达式；
(2)在 (1)的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围；
粤公网安备 44130202000953号