户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位全体720人中采用分层抽样的办法抽取50人进行了问卷调查,得到了如下列联表:
|
喜欢户外运动
|
不喜欢户外运动
|
合计
|
男性
|
20
|
|
|
女性
|
|
15
|
|
合计
|
|
|
50
|
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是 .
.
(Ⅰ) 请将上面的列联表补充完整;
(Ⅱ)求该公司男、女员各多少名;
(Ⅲ)是否有99.5﹪的把握认为喜欢户外运动与性别有关?并说明你的理由;
下面的临界值表仅供参考:

|
0.15
|
0.10
|
0.05
|
0.025
|
0.010
|
0.005
|
0.001
|

|
2.072
|
2.706
|
3.841
|
5.024
|
6.635
|
7.879
|
10.828
|
(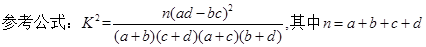 )
)