椭圆E的中心在坐标原点O,焦点在x轴上,离心率为 ,点P(1,
,点P(1, )和A、B都在椭圆E上,且
)和A、B都在椭圆E上,且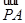 +
+ =m
=m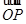 (m∈R).
(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.
推荐套卷
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为 ,点P(1,
,点P(1, )和A、B都在椭圆E上,且
)和A、B都在椭圆E上,且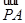 +
+ =m
=m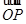 (m∈R).
(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.