如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
相关知识点
推荐套卷
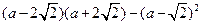 ,其中
,其中
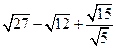
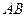 与
与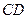 相交于点
相交于点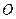 ,
,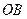 平分
平分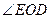 ,
,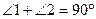 ,
, 
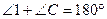 ,
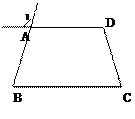
,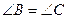 ,试说明:
,试说明: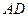 ∥
∥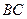 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号