如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）、D(2, n)三点．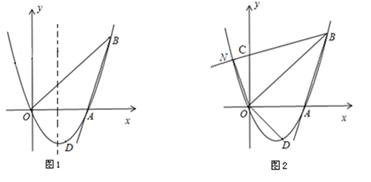
（1）求抛物线的解析式及点D坐标；
（2）点M是抛物线对称轴上一动点，求使BM－AM的值最大时的点M的坐标；
（3）如图2，将射线BA沿BO翻折，交y轴于点C，交抛物线于点N，求点N的坐标；
(4)在（3）的条件下，连结ON,OD，如图2，请求出所有满足△POD∽△NOB的点P坐标（点P、O、D分别与点N、O、B对应）．
相关试题
两种移动电话计费方式表如下：
| 全球通 |
神州行 |
|
| 月租费 |
15元/月 |
0 |
| 本地通话费 |
0．10元/分 |
0．20元/分 |
（1）一个月内某用户在本地通话时间为x分钟，请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用；
（2）若某用户一个月内本地通话时间为5个小时，你认为采用哪种方式较为合算？
（3）小王想了解一下一个月内本地通话时间为多少时，两种计费方式的收费一样多.请你帮助他解决一下.
相关知识点
推荐套卷
粤公网安备 44130202000953号