已知函数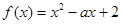
，
（
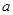为常数）
（1）当
时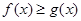
恒成立，求实数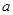的取值范围；
（2）若函数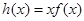
有对称中心为A（1，0），求证：函数
的切线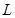
在切点处穿过图象的充要条件是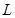恰为函数在点A处的切线．（直线穿过曲线是指：直线与曲线有交点，且在交点左右附近曲线在直线异侧）
推荐套卷
已知函数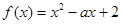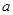，（为常数）
（1）当时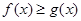恒成立，求实数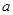的取值范围；
（2）若函数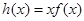有对称中心为A（1，0），求证：函数的切线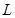在切点处穿过图象的充要条件是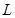恰为函数在点A处的切线．（直线穿过曲线是指：直线与曲线有交点，且在交点左右附近曲线在直线异侧）
粤公网安备 44130202000953号