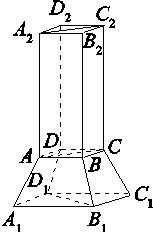
某个实心零部件的形状是如下图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台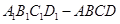 ,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱
,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱 .
.
(1)证明:直线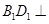 平面
平面 ;
;
(2)现需要对该零部件表面进行防腐处理.已知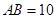 ,
,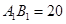 ,
,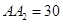 ,
, (单位:
(单位: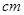 ),每平方厘米的加工处理费为
),每平方厘米的加工处理费为 元,需加工处理费多少元?
元,需加工处理费多少元?
推荐套卷
某个实心零部件的形状是如下图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台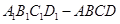 ,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱
,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱 .
.
(1)证明:直线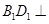 平面
平面 ;
;
(2)现需要对该零部件表面进行防腐处理.已知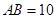 ,
,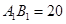 ,
,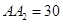 ,
, (单位:
(单位: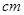 ),每平方厘米的加工处理费为
),每平方厘米的加工处理费为 元,需加工处理费多少元?
元,需加工处理费多少元?