已知圆A过点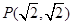
，且与圆B：
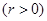关于直线
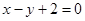对称.
(1)求圆A的方程；
(2)若HE、HF是圆A的两条切线，E、F是切点，求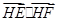
的最小值。
(3)过平面上一点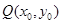
向圆A和圆B各引一条切线,切点分别为C、D，设
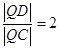，求证：平面上存在一定点M使得Q到M的距离为定值，并求出该定值.
相关试题
的底面为矩形，
，
，
分别是
的中点，
．
平面
；
平面
．
和
的交点，正方形一边所在直线的方程为
，求其他三边所在直线的方程.
．
平面
；
与
所成角的大小.
．
，试用定义证明：
在
上单调递增；
，当
时不等式
恒成立，求
的取值范围．
，点
是
轴上的一点，经过点
且斜率为
的直线
与抛物线相交于
两点．
的中点轨迹方程；
（
为坐标原点），求
的值．相关知识点
推荐套卷
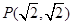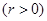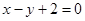已知圆A过点，且与圆B：关于直线对称.
(1)求圆A的方程；
(2)若HE、HF是圆A的两条切线，E、F是切点，求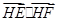的最小值。
(3)过平面上一点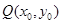向圆A和圆B各引一条切线,切点分别为C、D，设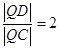，求证：平面上存在一定点M使得Q到M的距离为定值，并求出该定值.
粤公网安备 44130202000953号