已知数列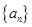 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时, .
.
(1)若 为偶数,且
为偶数,且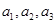 成等差数列,求
成等差数列,求 的值;
的值;
(2)设 (
( 且
且 N),数列
N),数列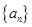 的前
的前 项和为
项和为 ,求证:
,求证: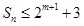 ;
;
(3)若 为正整数,求证:当
为正整数,求证:当 (
(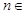 N)时,都有
N)时,都有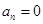 .
.
推荐套卷
已知数列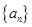 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时, .
.
(1)若 为偶数,且
为偶数,且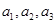 成等差数列,求
成等差数列,求 的值;
的值;
(2)设 (
( 且
且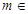 N),数列
N),数列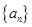 的前
的前 项和为
项和为 ,求证:
,求证: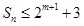 ;
;
(3)若 为正整数,求证:当
为正整数,求证:当 (
(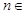 N)时,都有
N)时,都有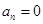 .
.