湖南省环保研究所对长沙市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数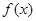
与时刻x的关系为
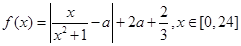，其中a是与气象有关的参数，且
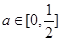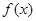，若用每天的最大值作为当天的综合放射性污染指数，并记作
.
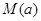(Ⅰ)令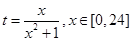
，求t的取值范围；
(Ⅱ)省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？
相关试题
均为锐角，且
，
．
的值；
的值．
为第三象限角，且
．
；
，求
，求
的值．
、
、
是同一平面内的三个向量，其中
．
，且
，且
与
垂直，求
．
＝
，
，
．若
是从集合A中随机取的一个实数，
是从集合B中随机取的一个实数，求关于
的方程
内，另一根在
外的概率．
的顶点坐标为
，
，
， 点P的横坐标为14，且
，点
是边
上一点，且
.
的值与点
的坐标；
为线段
（含端点）上的一个动点，试求
的取值范围.相关知识点
推荐套卷
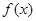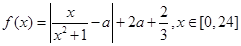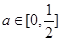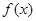湖南省环保研究所对长沙市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数与时刻x的关系为，其中a是与气象有关的参数，且，若用每天的最大值作为当天的综合放射性污染指数，并记作.
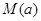(Ⅰ)令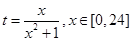，求t的取值范围；
(Ⅱ)省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？
粤公网安备 44130202000953号