在直角坐标系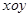 上取两个定点
上取两个定点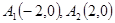 ,再取两个动点
,再取两个动点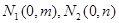 且
且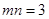 .
.
(I)求直线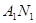 与
与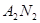 交点的轨迹
交点的轨迹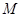 的方程;
的方程;
(II)已知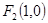 ,设直线:
,设直线: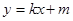 与(I)中的轨迹
与(I)中的轨迹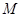 交于
交于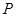 、
、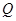 两点,直线
两点,直线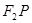 、
、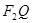 的倾斜角分别为
的倾斜角分别为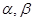 且
且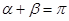 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标.
推荐套卷
在直角坐标系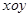 上取两个定点
上取两个定点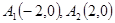 ,再取两个动点
,再取两个动点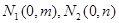 且
且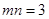 .
.
(I)求直线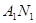 与
与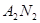 交点的轨迹
交点的轨迹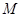 的方程;
的方程;
(II)已知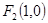 ,设直线:
,设直线: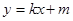 与(I)中的轨迹
与(I)中的轨迹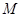 交于
交于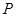 、
、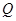 两点,直线
两点,直线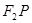 、
、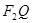 的倾斜角分别为
的倾斜角分别为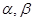 且
且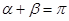 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标.