已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.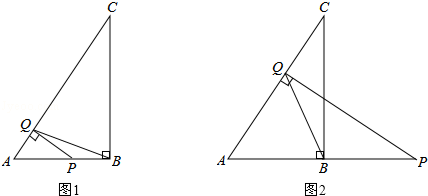
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
相关知识点
推荐套卷
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.