在数学课的学习中,我们已经接触了很多代数恒等式,知道可以用图形的面积来解释这些代数恒等式.如图①可以解释恒等式 ;
; 
(1)如图②可以解释恒等式 = .
= .
(2)如图③是由4个长为 ,宽为
,宽为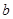 的长方形纸片围成的正方形,
的长方形纸片围成的正方形,
①用面积关系写出一个代数恒等式: .
②若长方形纸片的面积为3,且长比宽长3,求长方形的周长(其中a.b都是正数,结果可保留根号).
在数学课的学习中,我们已经接触了很多代数恒等式,知道可以用图形的面积来解释这些代数恒等式.如图①可以解释恒等式 ;
; 
(1)如图②可以解释恒等式 = .
= .
(2)如图③是由4个长为 ,宽为
,宽为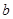 的长方形纸片围成的正方形,
的长方形纸片围成的正方形,
①用面积关系写出一个代数恒等式: .
②若长方形纸片的面积为3,且长比宽长3,求长方形的周长(其中a.b都是正数,结果可保留根号).