在直角坐标系xOy中,已知点P是反比例函数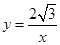 (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.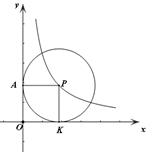
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:①求出点A,B,C的坐标;②反比例函数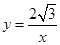 (x>0)图象上是否存在点M,使△MBP的面积是菱形ABCP面积的
(x>0)图象上是否存在点M,使△MBP的面积是菱形ABCP面积的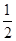 ,若存在,直接写出所有满足条件的M点的坐标;若不存在,试说明理由.
,若存在,直接写出所有满足条件的M点的坐标;若不存在,试说明理由.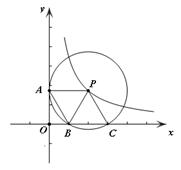
相关知识点
推荐套卷
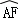 =
=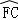 =
=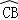 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
 ,求⊙O的半径.
,求⊙O的半径.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号