如图：矩形ABCD中，AB＝8，BC＝6，请在下图中画出面积不相等的三个菱形大致图形，使菱形的顶点都在矩形的边上，并直接写出你画的菱形的边长.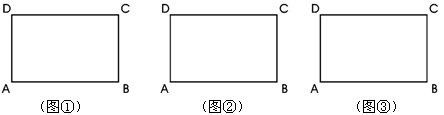
图①边长＝ ； 图②边长＝ ；图③边长＝ ；
此题中是否存在满足条件的面积最大的菱形？ （填“存在”或“不存在”）．
如图，在等腰梯形ABCD中，ABDC，AB=3
，DC=，高CE=2，对角线AC、BD交于H，平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移，分别交等腰梯形ABCD的边于M、N和R、Q，分别交对角线AC于F、G；当直线RQ到达点C时，两直线同时停止移动．记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2，若直线MN平移的速度为1单位/秒，直线RQ平移的速度为2单位/秒，设两直线移动的时间为x秒．
（1）填空：∠AHB= ；AC= ；
（2）若S2=3S1，求x；
（3）设S2=mS1，求m的变化范围．
已知，AB是⊙O的直径，点P在弧AB上（不含点A、B），把△AOP沿OP对折，点A的对应点C恰好落在⊙O上．
（1）当P、C都在AB上方时（如图1），判断PO与BC的位置关系（只回答结果）；
（2）当P在AB上方而C在AB下方时（如图2），（1）中结论还成立吗？证明你的结论；
（3）当P、C都在AB上方时（如图3），过C点作CD⊥直线AP于D，且CD是⊙O的切线，证明：AB=4PD．
观察下列等式：
12×231=132×21，
13×341=143×31，
23×352=253×32，
34×473=374×43，
62×286=682×26，
…
以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．
（1）根据上述各式反映的规律填空，使式子称为“数字对称等式”：
①52× = ×25；
② ×396=693× ．
（2）设这类等式左边两位数的十位数字为a，个位数字为b，且2≤a+b≤9，写出表示“数字对称等式”一般规律的式子（含a、b），并证明．
如图，二次函数y=（x﹣2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．
（1）求二次函数与一次函数的解析式；
（2）根据图象，写出满足kx+b≥（x﹣2）2+m的x的取值范围．
粤公网安备 44130202000953号