在△ABC中,AB=AC,∠BAC= (
(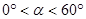 ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。
(1)如图1,直接写出∠ABD的大小(用含 的式子表示);
的式子表示);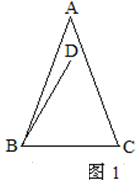
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求 的值。
的值。
相关知识点
推荐套卷
在△ABC中,AB=AC,∠BAC= (
(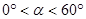 ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。
(1)如图1,直接写出∠ABD的大小(用含 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求 的值。
的值。