如图,四棱锥 的底面是正方形,
的底面是正方形,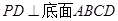 ,点
,点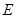 在棱
在棱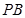 上.
上.
(1)求证:平面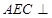 平面
平面 ;
;
(2)当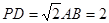 ,且
,且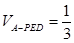 时,确定点
时,确定点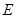 的位置,即求出
的位置,即求出 的值.
的值.
(3)在(2)的条件下若F是PD的靠近P的一个三等分点,求二面角A-EF-D的余弦值.
相关知识点
推荐套卷
如图,四棱锥 的底面是正方形,
的底面是正方形,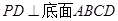 ,点
,点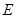 在棱
在棱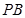 上.
上.
(1)求证:平面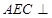 平面
平面 ;
;
(2)当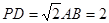 ,且
,且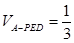 时,确定点
时,确定点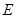 的位置,即求出
的位置,即求出 的值.
的值.
(3)在(2)的条件下若F是PD的靠近P的一个三等分点,求二面角A-EF-D的余弦值.