如图所示，扇形AOB,圆心角AOB的大小等于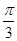
，半径为2，在半径OA上有一动点C，过点C作平行于OB的直线交弧AB于点P.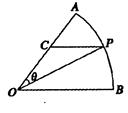
（1）若C是半径OA的中点，求线段PC的长；
（2）设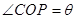
,求
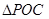面积的最大值及此时
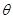的值.
相关试题
]时，f(x)的最大值为2，求a的值．
中，
，设
．
的前三项；
；
项和为
，
．
，直线 
，
与圆
交与
两点，点
.
时，求
的值；
时，求
为底面）被一平面所截得到的几何体，截面为
．已知
，
，
，
，
．
是
的中点，证明：
平面
的大小；
相关知识点
推荐套卷
如图所示，扇形AOB,圆心角AOB的大小等于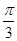，半径为2，在半径OA上有一动点C，过点C作平行于OB的直线交弧AB于点P.
（1）若C是半径OA的中点，求线段PC的长；
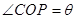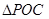（2）设,求面积的最大值及此时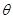的值.
粤公网安备 44130202000953号