如图，从
到
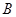有6条网线，数字表示该网线单位时间内可以通过的最大信息量，现从中任取3条网线且使每条网线通过最大信息量，设这三条网线通过的最大信息之和为
.
（1）当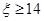
时，线路信息畅通，求线路信息畅通的概率；
（2）求的分布列和数学期望．
，
。
；（2）求
的最大值及相应的
值；
中，已知
，
，
．
的值；（Ⅱ）求
的值
，若
，且
和
的值；（II）求
的值。
．
，n
，试求|m
n|的最小值．
顶点的分别为
，
，
，其中
．
，求
的值；（2）若
，求推荐套卷
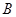如图，从到有6条网线，数字表示该网线单位时间内可以通过的最大信息量，现从中任取3条网线且使每条网线通过最大信息量，设这三条网线通过的最大信息之和为.
（1）当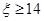时，线路信息畅通，求线路信息畅通的概率；
（2）求的分布列和数学期望．
粤公网安备 44130202000953号