某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段，已知跳水板
长为2m，跳水板距水面
的高
为3m，
=5m，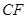
=6m，为安全和空中姿态优美，训练时跳水曲线应在离起跳点
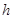m（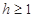
）时达到距水面最大高度4m，规定：以为横轴，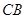
为纵轴建立直角坐标系.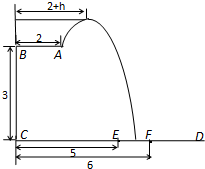
（1）当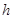=1时，求跳水曲线所在的抛物线方程；
（2）若跳水运动员在区域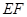
内入水时才能达到压水花的训练要求，求达到压水花的训练要求时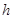的取值范围.
，
的值；
，
，求：
；（2）
.
与直线y=x+2
与复数
的共轭复数相等，求x，y.推荐套卷
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段，已知跳水板长为2m，跳水板距水面的高为3m，=5m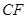，=6m，为安全和空中姿态优美，训练时跳水曲线应在离起跳点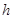m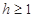（）时达到距水面最大高度4m，规定：以为横轴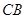，为纵轴建立直角坐标系.
（1）当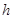=1时，求跳水曲线所在的抛物线方程；
（2）若跳水运动员在区域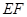内入水时才能达到压水花的训练要求，求达到压水花的训练要求时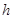的取值范围.
粤公网安备 44130202000953号