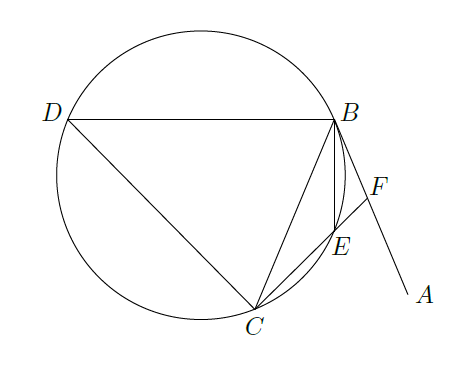
如图,直线
为圆的切线,切点为
,点
在圆上,
的角平分线
交圆于点
,
垂直
交圆于点
。
(Ⅰ)证明:
;
(Ⅱ)设圆的半径为
,
,延长
交
于点
,求
外接圆的半径。
推荐套卷
如图,直线
为圆的切线,切点为
,点
在圆上,
的角平分线
交圆于点
,
垂直
交圆于点
。

(Ⅰ)证明:
;
(Ⅱ)设圆的半径为
,
,延长
交
于点
,求
外接圆的半径。