某班一信息奥赛同学编了下列运算程序，将数据输入满足如下性质:
①输入1时，输出结果是
；
②输入整数
时，输出结果
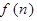是将前一结果
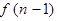先乘以3n-5，再除以3n+1.
（1） 求f(2),f(3),f(4);
（2） 试由（1）推测f(n)（其中
）的表达式，并给出证明.
相关试题
时，求不等式
的解集；
的解集包含
，求
的取值范围.
.
．
为整数）且关于
的方程
在区间
内有两个不同的实根，（1）求整数
的值；（2）若
时，总有
，求
的最大值。相关知识点
推荐套卷
某班一信息奥赛同学编了下列运算程序，将数据输入满足如下性质:
①输入1时，输出结果是；
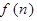②输入整数时，输出结果是将前一结果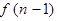先乘以3n-5，再除以3n+1.
（1） 求f(2),f(3),f(4);
（2） 试由（1）推测f(n)（其中）的表达式，并给出证明.
粤公网安备 44130202000953号