已知抛物线
，点P（-1，0）是其准线与
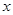轴的焦点，过P的直线
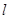与抛物线C交于A、B两点.
（1）当线段AB的中点在直线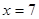
上时，求直线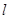的方程；
（2）设F为抛物线C的焦点，当A为线段PB中点时，求△FAB的面积.
是
的极值点，求
上的最小值和最大值；
上是增函数，求实数
的取值范围
与
；
的反函数
及
上是增函数
相关知识点
推荐套卷
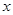已知抛物线，点P（-1，0）是其准线与轴的焦点，过P的直线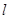与抛物线C交于A、B两点.
（1）当线段AB的中点在直线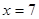上时，求直线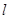的方程；
（2）设F为抛物线C的焦点，当A为线段PB中点时，求△FAB的面积.
粤公网安备 44130202000953号