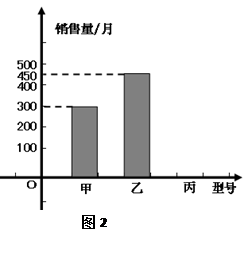
2013年6月6日第一届南亚博览会在昆明举行.某校对七年级学生开展了“南博会知多少?”的调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果分为“不太了解”、“基本了解”、“比较了解”、“非常了解”四个等级,对调查结果进行统计后,绘制了如下不完整的条形统计图:
根据以上统计图提供的信息,回答下列问题:
(1)若“基本了解”的人数占抽样调查人数的25%,此次调查抽取了 学生;
(2)补全条形统计图;
(3)若该校七年级有600名学生,请估计“比较了解”和“非常了解”的学生共有多少人?
相关知识点
推荐套卷
 (元) 、
(元) 、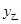 (元)与印制数量
(元)与印制数量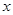 (本)之间的关系式;
(本)之间的关系式;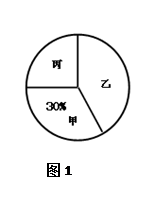
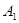 、
、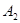 、
、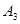 三条线路,从乙学校到丙学校有
三条线路,从乙学校到丙学校有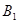 、
、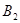 二条线路.
二条线路.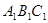 .请你画出旋转后的△
.请你画出旋转后的△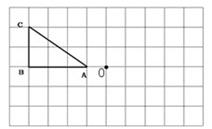

 粤公网安备 44130202000953号
粤公网安备 44130202000953号