如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG 的长为
A.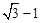 |
B.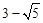 |
C.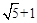 |
D.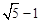 |
相关知识点
推荐套卷
如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG 的长为
A.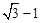 |
B.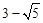 |
C.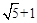 |
D.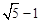 |