如图,AB是⊙O的直径,C是⊙0上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.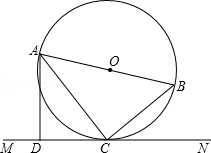
(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD=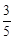 ,求⊙O的半径.
,求⊙O的半径.
推荐套卷
如图,AB是⊙O的直径,C是⊙0上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD=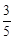 ,求⊙O的半径.
,求⊙O的半径.