我省某景区为提高经济效益，现对某一景点进行改造升级，从而扩大内需，提高旅游增加值，经过市场调查，旅游增加值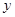
万元与投入
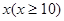万元之间满足：
为常数。当
万元时，
万元；
当
万元时，
万元。 （参考数据：
）
（1）求
的解析式；
（2）求该景点改造升级后旅游利润
的最大值。（利润＝旅游增加值－投入）。
相关试题
中．
平面
；
分别是
的中点，求证：平面
平面
．
（
，且
）．
的定义域和值域；
，求
的值．
中，
为
上不同于
的任一点， 
，求证：
平面
；（2）
．
，
．
*时，求
的子集的个数；
且
时，求
的取值范围．
．
；
，求实数a的取值范围．推荐套卷
我省某景区为提高经济效益，现对某一景点进行改造升级，从而扩大内需，提高旅游增加值，经过市场调查，旅游增加值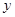万元与投入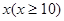万元之间满足：为常数。当万元时，万元；
当万元时，万元。 （参考数据：）
（1）求的解析式；
（2）求该景点改造升级后旅游利润的最大值。（利润＝旅游增加值－投入）。
粤公网安备 44130202000953号