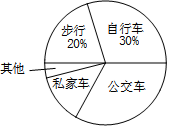
某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题: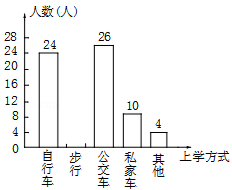
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
相关知识点
推荐套卷
 .
.
 的图像与一次函数
的图像与一次函数 的图像交于点A(m,2)和点B(-2, n ),一次函数图像与y轴的交点为C.
的图像交于点A(m,2)和点B(-2, n ),一次函数图像与y轴的交点为C.
 分别是等腰
分别是等腰 的腰
的腰 的中点.
的中点.
 边上求作一点
边上求作一点 ,使AM⊥BC(不写作法,保留作图痕迹)
,使AM⊥BC(不写作法,保留作图痕迹) ,其中
,其中 .
. 与
与 轴交于
轴交于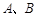 两点,与
两点,与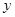 轴交于点
轴交于点 ,连结AC,若
,连结AC,若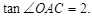

 上有一动点P,当
上有一动点P,当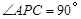 时,求出点
时,求出点 的坐标;
的坐标;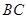 ,
,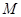 是线段
是线段 、
、 重合)的一个动点.过点
重合)的一个动点.过点 ,交抛物线于点
,交抛物线于点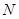 ,连结
,连结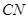 、
、 ,设点
,设点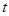 .当t为何值时,
.当t为何值时,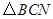 的面积最大?最大面积为多少?
的面积最大?最大面积为多少? 粤公网安备 44130202000953号
粤公网安备 44130202000953号