端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.
(1)请求出两种口味的粽子每盒的价格;
(2)设买大枣粽子x盒,买水果共用了w元.
①请求出w关于x的函数关系式;
②求出购买两种粽子的可能方案,并说明哪一种方案使购买水果的钱数最多.
相关知识点
推荐套卷
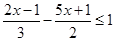 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.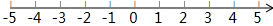
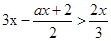 的解,求a的取值范围.
的解,求a的取值范围.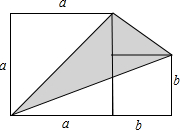

 粤公网安备 44130202000953号
粤公网安备 44130202000953号