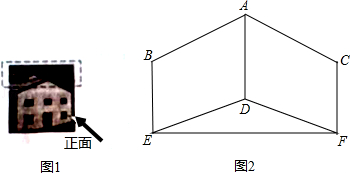
如图，图1是某仓库的实物图片，图2是该仓库屋顶（虚线部分）的正面示意图，BE、CF关于AD轴对称，且AD、BE、CF都与EF垂直，AD=3米，在B点测得A点的仰角为30°，在E点测得D点的仰角为20°，EF=6米，求BE的长．
（结果精确到0.1米，参考数据：
）
相关知识点
推荐套卷
如图，图1是某仓库的实物图片，图2是该仓库屋顶（虚线部分）的正面示意图，BE、CF关于AD轴对称，且AD、BE、CF都与EF垂直，AD=3米，在B点测得A点的仰角为30°，在E点测得D点的仰角为20°，EF=6米，求BE的长．
（结果精确到0.1米，参考数据：）
粤公网安备 44130202000953号