如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.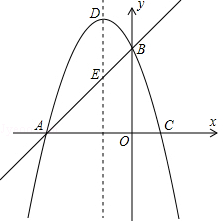
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
相关知识点
推荐套卷
 .
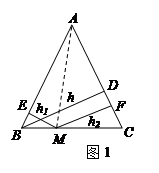
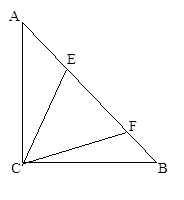
.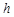 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为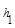 、
、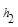 .连接AM,可得结论
.连接AM,可得结论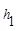 +
+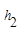 =
=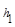 、
、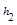 、
、
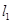 :
: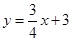 、
、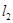 :
: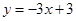 ,若
,若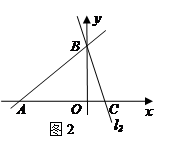
 四种型号的小轿车共1000辆进行展销.
四种型号的小轿车共1000辆进行展销.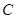 型号轿车销售的成交率为50%,其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中.
型号轿车销售的成交率为50%,其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中. 型号轿车有多少辆?
型号轿车有多少辆?
 粤公网安备 44130202000953号
粤公网安备 44130202000953号