设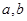 为实数,我们称
为实数,我们称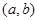 为有序实数对.类似地,设
为有序实数对.类似地,设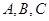 为集合,我们称
为集合,我们称 为有序三元组.如果集合
为有序三元组.如果集合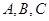 满足
满足 ,且
,且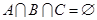 ,则我们称有序三元组
,则我们称有序三元组 为最小相交(
为最小相交(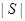 表示集合
表示集合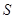 中的元素的个数).
中的元素的个数).
(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合 的子集构成的所有有序三元组中,令
的子集构成的所有有序三元组中,令 为最小相交的有序三元组的个数,求
为最小相交的有序三元组的个数,求 的值.
的值.
推荐套卷
设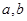 为实数,我们称
为实数,我们称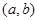 为有序实数对.类似地,设
为有序实数对.类似地,设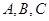 为集合,我们称
为集合,我们称 为有序三元组.如果集合
为有序三元组.如果集合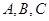 满足
满足 ,且
,且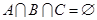 ,则我们称有序三元组
,则我们称有序三元组 为最小相交(
为最小相交(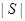 表示集合
表示集合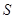 中的元素的个数).
中的元素的个数).
(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合 的子集构成的所有有序三元组中,令
的子集构成的所有有序三元组中,令 为最小相交的有序三元组的个数,求
为最小相交的有序三元组的个数,求 的值.
的值.